Physics FX Module 8
1. A wheel of diameter of 68.0 cm slows down uniformly from 8.40 m/s to rest over a distance of 115 m. What is the angular acceleration?
$v^2 = -2*a*s$ , $ a= -v^2/2/s =8.4^2/2/115 =-0.306 m/s^2$
$a =epsilon*R$, $epsilon = a/R = 2a/D = -2*0.306/0.68 = -0.902 rad/s^2$
correct answer is
D) $-0.90$ rad/s
2. A 1.0- object floats in water with 20% of it above the waterline. What does the object weigh out of the water?
80 % of the volume * water density = object mass
$M = 1000*0.8 =800 kg$, $G = M*g =800*9.81 =7848 N$
correct answer is
C) 7,840 N
3.

Figure 1 is a “snapshot” of a wave at a given time. The frequency of the wave is 120 Hz. What is (a) the amplitude, (b) the wavelength, and (c) wave speed?
Amplitude is 0.10 m as seen from the graphics. one full sinusoidal is between x = 0 and x = 0.20 m , it means $wavelength = 0.20$ m.
$wave-speed = wavelength/period = wavelength*Frequency =0.2*120 = 24$ m/s
4. A piece of aluminum with a mass of 1.0 kg and density of 2700 kg/m3 is suspended from a string and then completely immersed in a container of water. The density of water is 1000 kg/m3. (a) Determine the volume of the piece of aluminum.(b) Determine the tension in the string after the metal is immersed in the container of water.
$density = mass/volume$ , $volume = mass/density = 1/2700 = 3.7*10^{-4} m^3 =370 cm^3$
After immersion in water the piece of aluminum is pushed upwards with a force equal to the weight of the displaced water (Fa) and downwards by its weight (G)
$T = G-Fa = m*g – m_{water}*g =V*g*(rho – rho(water)) = 3.7*10^-4*9.81*(2700-1000) = 6.17 N$
5. On a 30°C day, there is an explosion. The sound is heard 3.4 s after seeing the flash. How far away was the explosion?
Speed of sound at 30 degree Celsius is 349.02 m/s. Speed of light is so big that we can consider it travel instantaneous.
$distance = speed of sound * time =349.02*3.4 =1186.7 m$
correct answer
D) 1.2 km
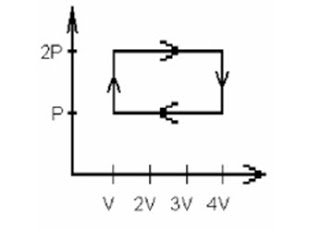
6. A gas is taken through the cycle illustrated here. During one cycle, how much work is done by an engine operating on this cycle?
infinitesimal work is $d W= P*d V$, $d V$ is the infinitesimal change of volume
At the constant volume (vertical transformations in the figure) there is no work done.
At the same pressure the work is
$W =2P*(4V-V) – P*(4V-V) = P*3V = 3PV$
correct answer
B) $3PV$
