Volume of Rotation (iintegrals)

6.
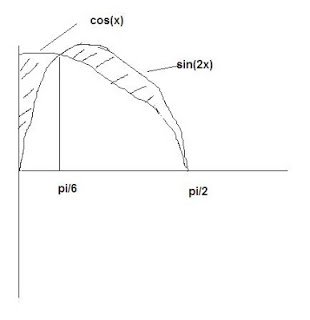
See the graph of the functions $cos(x)$ and $sin(2x)$ between 0 and $pi/2$ on the attached file.
the curves intersect where $cos(x) = sin(2x)$ , i.e.$ x = pi/6$
The area is
$A = int_0^pi/6 (cos(x) -sin(2x))d x + int_pi/6_pi/2 (sin(2x)-cos(x)d x) =$
$=[sin(x)+cos(2x)/2] (from 0 to pi/6) – [sin(x)+cos(2x)/2] (from pi/6 to pi/2) =$
$=sin(pi/6) +1/2*(cos(pi/3) -1) -[sin(pi/2) -sin(pi/6) +1/2*(cos(pi) -cos(pi/3)) =$
$=2*sin(pi/6) -sin(pi/2) + 1/2*cos(pi/3) -1/2 +1/2 +1/2*cos(pi/3) =$
$= 2*1/2 -1 + cos(pi/3) + 0=cos(pi/3) =1/2$
The correct answer is A)
17. The graph of $y= x^3$ intersects $y = 8$ at point $x =2$
the infinitesimal area under $x^3$ is $d A = x^3*d x$
By rotating this area about x =0 we get an infinitesimal volume of $d V = 2*pi*x*d A = 2*pi*x^4*d x$
The total volume of the figure under the curve $x^3$ and $y = 0$ is
$V = int_0^2) (2*pi*x^4*d x) = 2*pi*x^5/5 (from 0 to 2) = 64*pi/5$
Now the volume of the cylinder obtained by rotating x = 2 , y=8 about the y axis is
$V1 = pi*2^2*8 =32*pi$
The volume we are looking for is just the difference of the two volumes
$V2 = V1 – V = 32*pi-64*pi/5 =96*pi/5$
The correct answer is A)

12.
The position function is the integral of the speed function.
$s(t) = int[sin(omega*t)*cos^3(omega*t)*d t] = int[sin(x)*cos^3(x)*d x/omega] =$
$= int[sin(x)*(1-sin^2(x))*d(sin(x))/omega] =1/omega*[int(y*(1-y^2)*d y) =$
$=1/omega * [sin^2(x)/2 -sin^4(x)/4) + C$
$s(0)= 0$ it means $C =0$
$s(x) = 1/omega *(2sin^2(x) -sin^4(x))/4$ $x = omega*t$
correct answer is E)
