Quantum tunneling. Probability of transmission

A) Consider a particle incident left to right on a barrier potential, as in the figure. What is the particle’s wave- function if its energy is $E > V_o$? And if $E < V_o$? You do not need to complete the full calculation, but explain in detail how you would get to the result and draw the waveform, indicating clearly the difference between regions I,II and III.

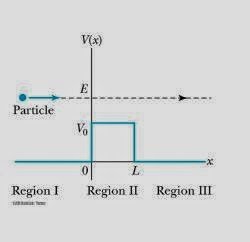
B) “Quantum tunneling” or ”barrier penetration” is not an experience of everyday life. A sprinter of mass 70 kg running at 5 m/s does not have enough kinetic energy to leap a wall of height 5 meters, even if all of that kinetic energy could be directed into an upward leap. If the wall is 0.2 meters thick, estimate the probability of the sprinter being able to ”quantum-tunnel” through it, rather than leaping over.

Answers

a) For the case $E>V0$ the wave function is a simple wave. Its general expression is

In region I)

$Psi(x) = A1*exp(i*k1*x) + A2*exp(-i*k1*x)$

(where k is the wave number and needs to be REAL)

First term $A1*exp(i*k1*x)$ is the transmitted part, second term $A2*exp(-i*k2*x))$ is the reflected term

$k1 = 2*pi/lambda = p/h_bar = sqrt{(2*m*E)/hbar}$

In region II) we have

$Psi(x) = B1*exp(i*k2*x)+B2*exp(-i*k2*x)$

$k2 = 2*pi/lambda =p/hbar =sqrt{(2*m*(E-V0))/hbar}$

In region III)

$Psi(x) = C1*exp(i*k3*x) +C2*exp(-ik3*x)$

$k3 = 2*pi/lambda = p/hbar = sqrt{(2*m*E)/hbar}$

The coefficients need to satisfy the continuity conditions for Psi(x) and $d Psi/d x$ at $x =0$ and $x=L$

That is:

$A1+A2 = B1+B2$

$B1*exp(i*k2*L) +B2*exp(..) =C1*exp(i*k3*L) +C2*exp(..)$

or rewritten

$i k_1A_1 -i k_2A_2 =i k_2B_1 -i k_2B_2$

$i k_2B_1*exp(i k_2L) -i k_2B_2exp(-i k_2L) = i k_3C_1*exp(i k_3L) -i k_3C_2*exp(…)$

b) in this case $(E < V0)$ only the expression in region II is modified from above. In region I and III) there will be the same expressions for Psi as above.

In region II we have)  $(V0  > E)$ an exponential real function

$Psi(x) = B1*exp(k2*x) +Bx*exp(-k2*x)$

where k2 is the wave number REAL

$k2 = sqrt{(2*m*(V0-E))/ hbar}$

The same conditions for Psi(x) and $d Psi/d x$ at $x=0$ and $x =L$ apply

Question B) with sprinter

Suppose one has only the transmitted wave

In region I) we have a wave $Psi(x) = A*exp(i*k1*x)$

In region II) an exponentially decreasing function $Psi(x) = B*exp(-k2*x)$

In region III) we have again the direct transmitted wave $Psi(x) = C*exp(i*k3*x)$

Continuity of $Psi(x)$ at $x= 0$ and $x =L$

$A =B$

$B*exp(-k2*L) =C*exp(i*k3*L)$

$C = A*exp(-k2*L)/exp(i*k3*L) = A*exp(-k2*L)*exp(-i*k3*L)$

The ratio of the amplitudes of wave-function in regions III and I) is:

$Psi_III/Psi_I = C*exp(ik3x)/A*exp(i*k1*x)$

The probability of tunneling (coefficient of transmission) is just the square of the modulus of the ratio:

$T = | Psi_III/Psi_I |^2 = |C/A|^2 = exp(-2*k2*L)$

$V0 = m*g*h =70*9.81*5 =3433.5 J$

$E =m v^2/2 =70*5^2/2 = 875 J$

$L =0.2 m$

$k2 = sqrt{(2*m*(V0-E))/hbar} =sqrt{(2*70*(3433.5-875)) /10^{-34}} =6*10^{36}$

$T =exp(-2*k2*L) = exp(-2*6*10^{36}*0.2) =…..$

The windows scientific calculator can not compute such a small value.