Icy slope and sled
The icy slope
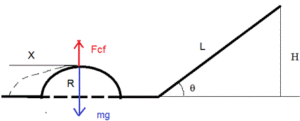
A frictionless icy slope of angle $\theta$ having a length $L$, followed by a horizontal portion, then by a bump ($R$) make a frictionless path as in the image. The weight of the sled on this path is C*TrueWeight when the sled is exactly at the bump’s top, ($0 < = C < 1$).
a) Please find the value of R as function of $C$, $\theta$ and $L$.
b) Find $R=?$ when $\theta=26 deg$, $C = 0.75$, and $L = 5 m$.
c) When $C = 0$, the sled jumps at the top of the bump. What is the horizontal distance that the sled travels as a function of $L$, $R$, $\theta$ and $g$.
Continue reading on physics forums….
The bump
At the top of the bump the total force is the difference between the sled weight and the centrifugal force. The centrifugal force acts outside the path.
$C*(mg)=mg-F_cf=mg-(mv^2)/R$
From the energy conservation considerations we write the equation:
$mgH=(mv^2)/2+mgR so mv^2=mg(2H-R)$
where we find the initial height from the equation:
$H=L*sinθ$
Thus the dependence of $R$ on the $L$, $\theta$ and $R$ is
$C(mg)=mg-mg/R*[2L*sin (θ-R)]$
$C=1-1/R*(2L*sin (θ-R))$ or $C=1-2*(L/R)*sinθ+1$ or $C-2=-2(L/R)*sinθ$
$R=(2L*sinθ)/(2-C)$
b)
With the values from text we find for $R$,
$R=(2*5*sin 26)/(2-0.75)=3.50 m$
Range of sled
c)
At the top of the bump the speed is
$v=\sqrt{g(2H-R)}=\sqrt{g[2L*sin θ-(2L*sinθ)/2)] }=\sqrt{gL*sinθ}$
(We can apply also energy considerations to find this.)
Thus, the time to fall from height R (on top of bump) is
$R=(gt^2)/2$ so $t=\sqrt(2R/g)$
Finally, the range of the sled after it jumps over the top of the bump is the product of the speed with the time:
$X=v*t=\sqrt{gL*\sin θ*(2R/g)}=\sqrt{2LR*\sin θ }$
Observation: On all frictionless paths, one can apply the principle of conservation of energy to find the unknown values (for example the final speed). (The initial potential energy = Final kinetic energy+…)