Circle with charge (Griffiths)

You are given a circle in the (x y) plane that has a homogeneously distributed charge:

a) What is the potential $V$ on the $z$ axis?

b) What is the electric field on the $z$ axis?

c) Where is the field maximal?

d) What are the values of $V$ and $E$ at this point if $q=10^{-8} C$ and $a=2 cm$?

Show My Homeowork - Circle with Charge

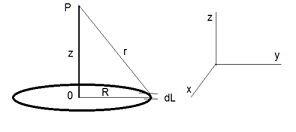
$d q=q* d L/(2πR)$

$d V(P)=k*d q/r=k q d L/2πR*1/sqrt{z^2+R^2}$

Potential is scalar so adds algebraically:

$V(P)= ∫_0^L d V(P)=k q/2πR ∫_0^L d L*1/sqrt{z^2+R^2}=$

$=k q/2πR*2πR*1/sqrt{z^2+R^2}=k q/sqrt{(z^2+R^2 )}$

Potential is maximal at

$d V/dz=0$  or $-k q z/sqrt{(z^2+R^2 )^3 }=0$  or $z=0$

$V(z=0)=k q/R=(9*10^9*10^{(-8)})/(2*10^{(-2)} )=(9/2)*10^3=4.5*10^3  V$

Field is

$E(P)=-∇V(P)=-d/dz V(P)=k q z/sqrt{((z^2+R^2 )^3)}$    along z axis
Field is maximum at

$d E/dz=0$  or  $(2z^2-R^2)/sqrt{((z^2+R^2 )^3})=0$   or $z=±R/sqrt{2}=±2/sqrt{2}=±√2 cm$

$E(z=√2  cm)=[(9*10^9*10^{-8}*√2*10^{-2})] / sqrt{((2+4)^3*10^{-12}})=$

$=(9√2*10^{-1})/(6√6*10^{-6})=3/(2√3)*10^5=√3/2*10^5$  (V/m)

$V(z=√2  cm)=(9*10^9*10^{-8}) / (sqrt{2+4}*10^{-2} )=[9/sqrt{6}]*10^3$  V