Stromboli Eruption
The Stromboli Volcano
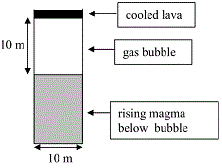
When the Stromboli volcano is active a big gas bubble rise up in the volcano lava. At some moment when the pressure of the bubble is big, it expands isotropically and emerges at the surface of the lava.
(a) A cylindrical bubble having a pressure of 3.3 atm, a height and diameter of 10 m when is starting to expand inside Stromboli until the atmospheric pressure. Please find the initial and final volumes of the bubble. Inside the bubble the gas has $\gamma=1.28$ (steam or $H_2O$ has 7 degrees of freedom because it is a triatomic molecule). (b) Please find the work of the gas in its expansion.
(c) If all this work is done at the surface of Stromboli volcano in a cylindrical region of 10 m diameter, h=0.5m and $\rho=2000 kg/m^3$ and if all of this lava has the same final velocity $v$, what is $v$?
You can continue reading on this volcano
The infinitesimal work
a) The infinitesimal work for all types of transformations is by definition the product between the pressure and the volume change. Hence:
$d W=p dV$
For the adiabatic transformation specified in the text one has the equation of state:
$P_1V_1^{\gamma}=P_2V_2^{\gamma}(=C)$
As a result, in general we use the equation:
$P=C/V^{\gamma}=(P_1V_1^{\gamma})/V^{\gamma}$ and $V_2=V_1(P_1/P_2)^{1/\gamma}$
that is re-written as,
$(V_1/V_2)^{\gamma-1}=(P_2/P_1)^{(\gamma-1)/\gamma}$
The initial volume of the gas bubble is
$V_1=\pi R^2H=\pi*5^2*10=785.40 m^2$
and so the final volume of gas is
$V_2=785.4(3.3/1)^{1/1.28}=1996.09 m^3$
Entire work
b)
To find the entire work one has to integrate the previous equation
$W_{12}=\int _{V_1}^{V_2} P d V=P_1V_1^{\gamma}\int_{V_1}^{V_2}d V/V^{\gamma}=$
$=P_1V_1^{\gamma}*1/[(1-\gamma)V^{\gamma-1}] |_{V_1}^{V_2}$
$W_{12}=P_1V_1^{\gamma}/(\gamma-1)*[(1/V_1^{\gamma-1})-(1/V_2^{\gamma-1})]=P_1V_1/(\gamma-1)[1-(V_1/V_2)^{\gamma-1}]$
$W_{12}=[P_1V_1/(\gamma-1)]*[1-(P_2/P_1)^{(\gamma-1)/\gamma}]$
from the text we have the values $P_1=3.3 atm=3.3*10^5 (N/m^2)$, $P_2=1 atm=10^5 N/m^2$ and $V_1=\pi R^2H=\pi*5^2*10=785.40 m^3$ and $\gamma=1.28$
$W_{12}=(3.3*10^5*785.4)/(0.28)(1-(1/3.3)^{0.28/1.28}=2.128*10^8 J$
Lava speed
c)
The mass of lava is the product between the density and its volume,
$m=\rho V=\rho*\pi R_1^2 H=2000*\pi*5^2*0.5=78539.8 kg$
so we can find the final speed from the kinetic energy:
$W_{12}=mv^2/2$ that is $v=\sqrt{2W_{12}/m}=…=73.61 m/s$